(백준/C++) 11660_구간 합 구하기 5

11660번: 구간 합 구하기 5 (acmicpc.net) 문제는 2차원 배열에서 누적 합을 통해 특정 구간의 합을 빠르게 계산하기 위한 방법을 묻는 문제입니다.

누적 합 문제는 구간에 있는 수의 합을 빠르게 계산하기 위한 방법입니다.

이를 이용하면 $O(N^2)$의 시간 복잡도로 누적 합 배열을 생성하고, 특정 구간의 합을 $O(1)$의 시간 복잡도로 계산할 수 있습니다.

---

로직 설계

이 문제는 먼저 11659번: 구간 합 구하기 4 (acmicpc.net) 문제를 풀고 오는 것을 추천 드립니다.

이 문제는 $(x1, y1)$부터 $(x2, y2)$까지 합을 구하는 문제입니다.

(백준/C++) 11659_구간 합 구하기 4 풀이 글

1차원 구간 합의 개념

2차원 구간 합을 구하기 전에 먼저 구간 합을 구하는 방법부터 보겠습니다.

(3~4) 구간은 (1~4) 구간에서 (1~2) 구간을 빼는 것으로 구할 수 있습니다.

따라서, 만약 수를 누적 해 저장한다고 한다면, 두 누적 합의 계산만으로 구간 합을 쉽게 구할 수 있게 됩니다.

2차원 구간 합의 개념

위 개념을 응용한다면, 2차원 구간 합을 구하는 방법도 어렵지 않게 생각할 수 있습니다.

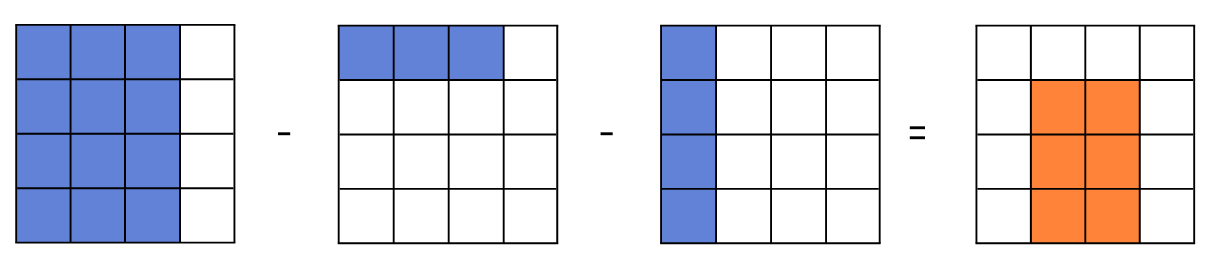
예를 들어, (2, 2)부터 (3, 4)까지 합을 구하기 위해서는 (3, 4)까지 합에서 (3, 1)까지의 합과 (1, 4)까지의 합을 빼는 것으로 구할 수 있습니다.

---

풀이

누적 합을 저장할 때, 저는 바로 위의 누적 합과 왼쪽의 누적 합을 더해서 계산 했습니다.

이때, 겹치는 구간이 존재하기 때문에 sum[i - 1][j - 1] 을 빼서 저장했습니다. 이렇게 함으로써, 중복으로 합산되는 부분을 제거할 수 있습니다.

또한, 누적 합을 계산할 때에도 마찬가지로 위쪽과 왼쪽의 누적 합을 빼는데, 겹치는 구간이 존재하기 때문에 이 부분도 sum[x1 - 1][y1 - 1] 을 더하는 것으로 계산 했습니다.

#include <iostream>
using namespace std;

int sum[1025][1025];

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);

	int N, M;
	cin >> N >> M;

	// 2차원 정수 입력 받으며 합산하기
	for (int i = 1; i <= N; i++)
	{
		for (int j = 1; j <= N; j++)
		{
			cin >> sum[i][j];
			sum[i][j] += sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1];
		}
	}

	//범위 계산
	while (M--)
	{
		int x1, y1, x2, y2;
		cin >> x1 >> y1 >> x2 >> y2;
		cout << (sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1]) << '\n';
	}
}