(백준/C++) 11729번_하노이 탑
하노이의 탑 문제는 재귀 문제의 대표주자격 문제입니다.
11729번: 하노이 탑 이동 순서 (acmicpc.net) 문제는 3개의 기둥과 그 위에 있는 서로 다른 크기의 원반이 주어지고, 첫 번째 기둥에서 세 번째 기둥으로 모든 원반을 이동시키는 것이 목표입니다.
이때, 두 가지 규칙이 존재하는데,
- 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
- 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이러한 제한 사항 하에서 원반을 모두 옮기는 최소의 이동 횟수와 그 과정을 출력하는 문제입니다.
접근법
제가 예전에 처음 이 문제를 풀었을 때에는 재귀적으로 생각하지 못했었습니다.
제가 처음 본 접근법이 아래와 비슷한 내용이었습니다.
n개의 원판이 있을 때, 가장 큰 원판을 제외한 나머지 원판들을 2번째 기둥으로 옮긴 후, 가장 큰 원판을 3번째 기둥으로 옮깁니다. 그리고 2번째 기둥에 있던 원판들을 다시 3번째 기둥으로 옮기면 됩니다. 이러한 과정은 원판의 수가 1개일 때까지 반복됩니다.
저는 이 내용이 어렵다고 느껴졌습니다.
따라서 제가 이 문제를 몇 번 풀어보면서 정리한 내용을 풀어 설명해 드리도록 하겠습니다.
이 문제의 핵심은 2개입니다.
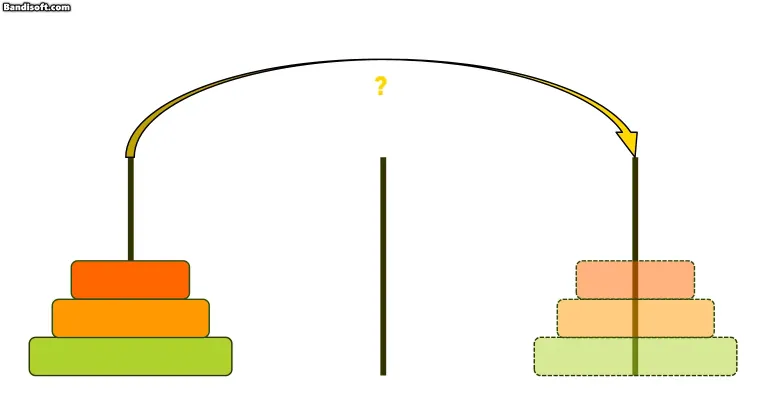
① 우선, N개의 원반을 목표 지점(3)에 놓기 위해서는 N-1개의 원반을 임시 기둥에 놓아야 합니다.
목표 기둥에 옮기기 위해서는 큰 원반을 먼저 옮기고 나머지 N-1개의 원반을 옮겨야 한다.
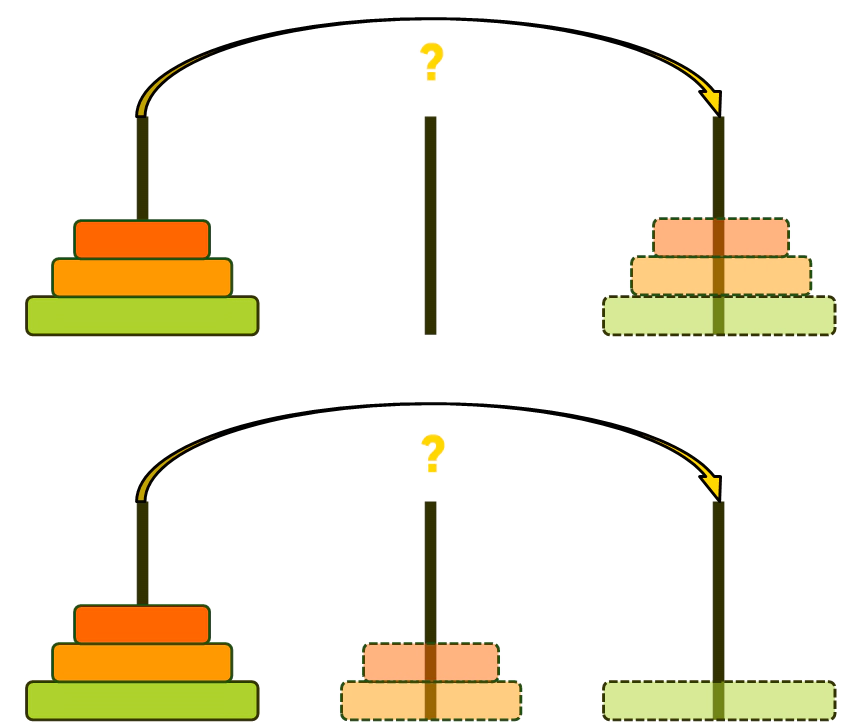
② 마찬가지로 N-1개의 원반을 임시 기둥(목표 기둥)에 두기 위해서는 (N-1)-1개의 원반을 또 다른 기둥(임시 기둥)에 두어야 할 것입니다.
따라서 새로운 (N-1)-1개의 원반에 대해서 새로운 하노이 해법을 찾는 것이 이 문제의 첫 번째 핵심입니다.
즉, N-1개의 원반을 서로 다른 기둥에 번갈아 두는 해법을 재귀로 찾아가고, 마지막 남은 원반부터 옮기기 시작할 것입니다. 이 부분이 핵심인 재귀 부분입니다.
③ 1개의 원반이 남았을 때, 원반을 옮기기 시작합니다.
④ 이때, N개의 원반을 옮기려고 임시 기둥에 놓았던 N-1개의 원반을 다시 가장 큰 원반의 위에 옮기기 위한 풀이를 찾아야 합니다.
기존에 1번 기둥에 있던 원반을 목표 기둥에 두는 것과는 다르게 임시 기둥에 두었던 N-1개의 원반을 다시 큰 원반 위에 옮기는 방법을 찾는 것이 마지막 핵심입니다.
결국 이것도 N-1개의 원반을 원하는 기둥에 옮기는 것은 하노이 해법을 찾아가는 것과 같습니다.
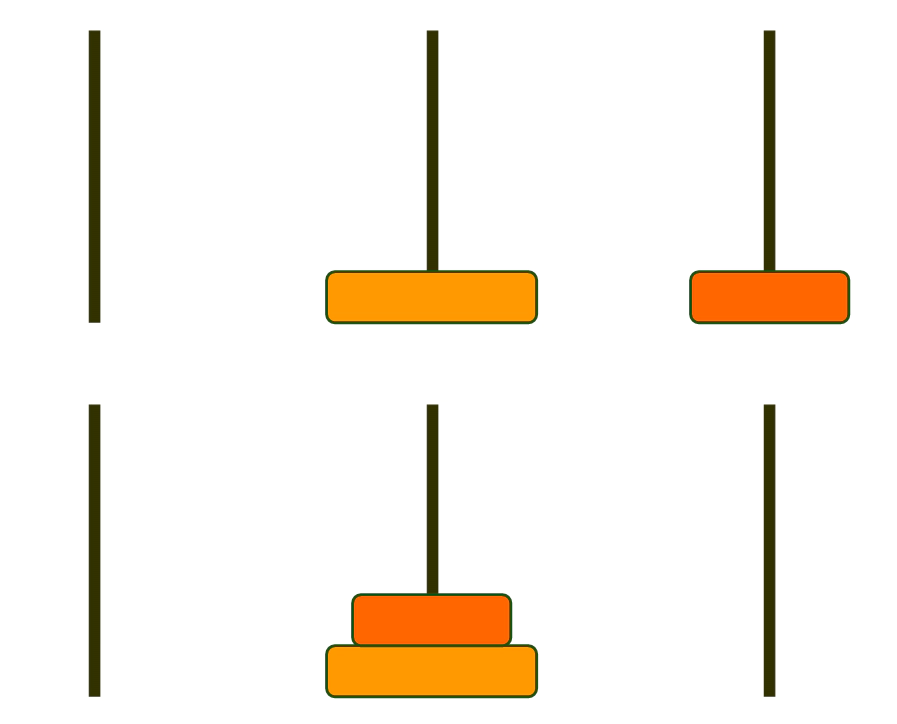임시 기둥에 두었던 N-1개의 원반(이미지에서는 1개)를 큰 원반의 위에 옮기는 해법을 찾아야 한다.
정리하자면,
- N개의 원반을 목표 기둥에 두기 위해
N-1개의 원반을임시 기둥에 두는 해법을 찾아갑니다. - 큰 원반을 옮겼다면
- 큰 원반을 옮기기 위해
임시 기둥에 두었던 N-1개의 원반을 큰 원반이 있는목표 기둥에 두는 해법을 찾아갑니다.
풀이
접근법이라기보다 풀이처럼 되어버렸지만, 제가 이 문제를 처음 풀었을 때에도 여전히 문제를 이해하지 못했던 기억이 나서… 문제를 푸는데 많은 도움이 되었으면 좋겠다는 생각에 이것저것 설명드리고 싶었습니다.
아래는 코드입니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
using namespace std;
// n개의 원반을 시작 기둥(s)에서 도착 기둥(d)로 이동시킵니다.
// 이때, 임시 기둥(t)을 사용합니다.
void Hanoi(int n, int s, int t, int d)
{
if (n < 1) return;
Hanoi(n - 1, s, d, t); //N개의 원반을 목표 기둥에 두기 위해 N-1개의 원반을 임시 기둥에 두는 해법을 찾아갑니다
cout << s << ' ' << d << '\n'; //가장 큰 원반을 시작 기둥에서 도착 기둥으로 이동시킵니다.
Hanoi(n - 1, t, s, d); //큰 원반을 옮기기 위해 임시 기둥에 두었던 N-1개의 원반을 큰 원반이 있는 목표 기둥에 두는 해법을 찾아갑니다.
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
int N;
cin >> N;
cout << ((1 << N) - 1) << '\n';
Hanoi(N, 1, 2, 3);
}
설명이 명확했는지는 모르겠지만 많은 도움이 되었으면 좋겠습니다.