(백준/C++) 1904_01타일
1904번: 01타일 문제는 동적 계획법으로 풀 수 있는 문제입니다.
동적 계획법(Dynamic Programming, DP)이란, 큰 문제를 작은 문제들로 나누어 풀어나가고 작은 문제의 해를 저장해 다시 계산하지 않고 사용하는 방식입니다.
동적 계획법 문제는 최적 부분 구조와 중복된 부분 문제의 두 가지 속성을 가진 문제에 유용합니다.
01타일 문제에서 가장 먼저 고려해야 할 부분은 “00” 타일과 “1” 타일의 특성입니다. “00” 타일은 가로 길이 2, “1” 타일은 가로 길이 1이라는 점을 확인해야 합니다.
그래서 이 둘을 조합해 나가면서 N 길이의 2진 수열을 만드는 방법의 수를 찾아나가야 합니다.
- 최적 부분 구조: 즉, 01타일 문제에서 길이 N인 2진 수열을 만드는 경우의 수를 찾으려면, 길이 N-1과 길이 N-2의 2진 수열을 만드는 경우의 수로부터 해를 구해야 합니다.
- 중복된 부분 문제: 길이가 N-2인 경우의 수와 길이가 N-1인 경우의 수를 계속해서 구해야 하는 중복된 부분 문제가 발생하는 구조입니다. 예를 들어 길이가 N인 2진 수열의 경우의 수를 구하기 위해서는 N-2와 N-1의 경우의 수를 구해야 하고, 그 N-2와 N-1의 경우의 수도 거기에서 N-2와 N-1의 경우의 수를 구해야 합니다.
접근 방법
1. Tabulation(Bottom-up) 식 생각하기
우선, N=1 과 N=2 인 경우는 타일의 특성에 의해 정해져 있다고 할 수 있습니다. 따라서 N=3 부터 시작해서 타일들을 하나씩 추가해가며 가능한 수를 생각합니다.
즉, 2진 수열의 끝에 “1” 타일을 추가하는 경우와 “00” 타일을 추가하는 경우를 더해가며 계산한다고 보면 되겠습니다.
2. 점화식 찾기
이제 위 경우에 대한 점화식을 찾아야 합니다.
만약 이 문제를 처음 접하게 되면 이 문제를 어떻게 점화식으로 표현하지? 하는 생각이 들 수 있습니다.
따라서 이 부분은 이미지와 함께 설명 드리도록 하겠습니다.
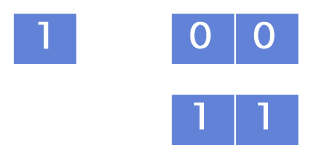
1) 우선 N=1인 경우와 N=2인 경우를 먼저 생각해 봅시다.
이때 잘 보면 “11”의 경우에는 “1”에서 “1”을 추가한 것이라고 볼 수 있을 겁니다.
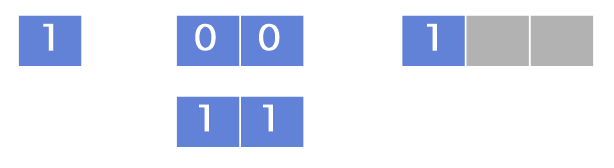
2) 이제 타일을 추가해야 하는데, 먼저 “00” 타일을 추가한다고 생각해 봅니다.
“00” 타일을 추가하기 위해서는 N이 2 증가 되어야 합니다. (즉, 빈 칸이 2칸이 되어야 합니다.) 따라서, N=1인 타일에만 추가할 수 있을 겁니다.
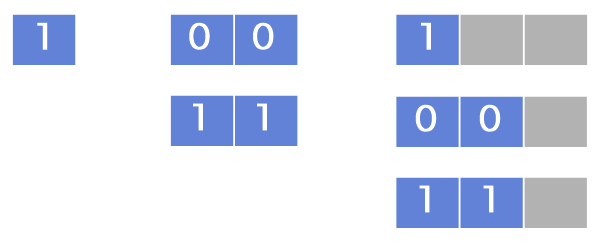
3) 아직 N=3 인 경우가 끝난게 아닙니다. “1” 타일을 추가하는 경우가 남아있기 때문입니다.
“1”타일을 추가하기 위해서는 N이 1 증가 되어야 합니다. (즉, 빈 칸이 1칸이 되어야 합니다.)
이제 점화식을 작성하실 수 있을겁니다. 하지만, 혼자서 이 점화식을 찾다보면 헷갈리는 경우가 생기게 됩니다.
제 경우에는 두 가지 사소한 의문이 들었었습니다.
- “11”을 추가하는 경우는 어떻게 되는거지?
- 앞에 타일을 추가하는 경우는 생각하지 않아도 되는거야?
이 두 개의 의문을 해결해드리겠습니다.
1의 경우, “11” 타일은 “1” 타일을 추가한 이후 다음 N에서 “1” 타일을 추가한 것과 같습니다. 이 의문은 순전히 여러 경우의 수를 생각하다가 너무 깊이 생각해버려서 순간적으로 헷갈린 의문이었습니다.
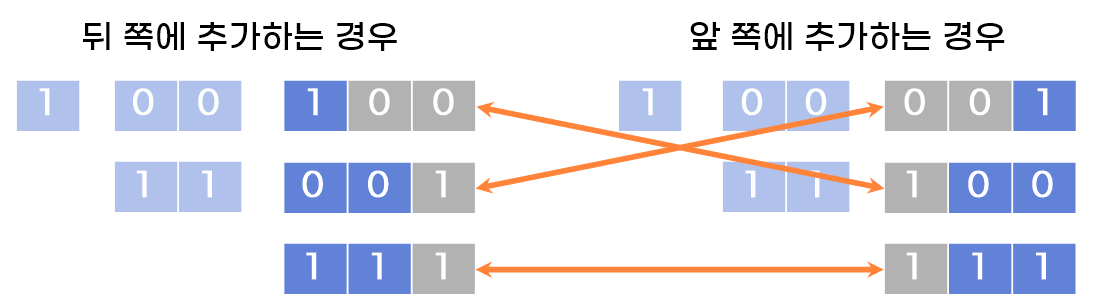
2의 경우, 앞 쪽에 타일을 추가하는 로직과 뒤 쪽에 타일을 추가하는 로직이 결과적으로 같다는 것입니다.
이 의문은 직접 그려가면서 알게 되었는데, 한 번 직접 그려보는 것도 좋을 것 같습니다.
이미지로 보자면 뒤 쪽에 추가하는 경우와 앞 쪽에 추가하는 경우 순서만 달라질 뿐 같은 수가 됩니다.
풀이
점화식을 찾으셨나요?
점화식은 arr[N] = arr[N-1] + arr[N-2] 였습니다.
여기서 arr[N-1]은 길이가 N-1인 수열 뒤에 ‘1’ 타일을 추가한 경우, arr[N-2]는 길이가 N-2인 수열 뒤에 ‘00’ 타일을 추가한 경우로,
각각의 추가 가능한 경우의 수가 각각 N-1의 수, N-2의 수와 같습니다.
따라서, 해당 점화식으로 N이 3부터 N까지 구하는 코드를 작성하면 됩니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
#include <vector>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
int N;
cin >> N;
vector<int> arr(N >= 3 ? N : 3);
arr[0] = 1; //1
arr[1] = 2; //00, 11
for(int i = 2; i < N; i++)
{
arr[i] = (arr[i - 2] + arr[i - 1]) % 15746;
// arr[2] = 100 [i-2 + "00"], 001, 111 [i-1 + "1"]
}
cout << arr[N - 1];
}