(백준/C++) 1992_쿼드트리

1992번: 쿼드트리 (acmicpc.net) 문제는 분할 정복(Divide and Conquer) 문제입니다.

분할 정복은 큰 문제를 작은 부분 문제로 나누어 해결하고, 그 결과를 합쳐 원래 문제의 해결책을 찾는 방법입니다.

이 문제는 이전 색종이 만들기 문제를 풀었다면, 쉽게 풀 수 있는 문제입니다.

2630번: 색종이 만들기 (acmicpc.net)

이 문제를 조금 풀어서 설명하자면, 0과 1로 된 구조를 4개의 동일한 크기의 영역으로 분할하고, 각 영역이 동일한 데이터를 가지면 해당 데이터로 표현해 달라는 문제입니다.

여기에서 압축하면 나오는 결과 값은 분할 단계(깊이)라고 보시면 될 것 같습니다.

출처: 백준 - https://www.acmicpc.net/problem/1992

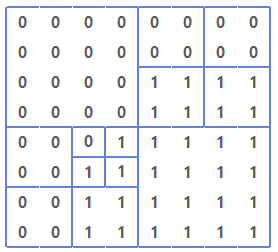
이렇게 된 구조를 4개 영역으로 분할하면서 풀어가다 보면 다음과 같은 결과가 나옵니다.

쿼드트리 문제를 색종이 문제로 풀어본 결과

이 결과를 분할 단계로 묶어보면 “(0(0011)(0(0111)01)1)”로 표현될 수 있다는 것을 알 수 있습니다.

---

접근법

분할 정복(Divide and Conquer)은 세 가지 접근법으로 먼저 생각해볼 수 있습니다.

바로, 분할 - 정복 - 결합 입니다.

1) 분할(Divide)

현재 영역의 데이터가 모두 같은 값인지 확인합니다.

만약 모두 같은 값이 아니라면, 데이터를 왼쪽 위, 오른쪽 위, 왼쪽 아래, 오른쪽 아래, 이렇게 4개의 동일한 크기의 종이로 나누어 갑니다.

2) 정복(Conquer)

각 부분 문제에 대해 같은 방법으로 재귀적으로 문제를 해결합니다.

즉, 각 부분이 모두 같은 값으로 나눠졌는지 확인하고, 그렇지 않다면 다시 4개의 부분으로 나눕니다.

기저 사례(Base Case): 만약 데이터가 하나의 값으로 압축시킬 수 있다면 해당 데이터 값을 즉시 반환합니다.

3) 결합(Combine)

정복 단계의 결과를 합쳐 최종 결과를 출력하는 단계입니다.

이 문제에서는 각 영역의 압축 결과를 괄호로 묶어 표현하고, 이를 연결하여 최종 압축 문자열을 생성합니다.

---

풀이

이 문제는 각 압축 단계에서 결과를 바로 출력할 수 있기 때문에 결합 단계를 만들지 않아도 풀 수 있습니다.

즉, 각 정복 단계에서 깊이(분할 단계)를 증가시키기 전에 괄호를 출력하고, 각 단계(4개의 영역)의 정복이 끝난 이후 닫는 괄호를 출력시켜 주는 것으로 결합이 종료될 수 있습니다.

#include <iostream>
using namespace std;

int img[64][64];

struct coord
{
	int x;
	int y;
};

coord getMid(const coord& A, const coord& B)
{
	return { (A.x + B.x) / 2, (A.y + B.y) / 2 };
}

void solve(const coord& start, const coord& end)
{
	if((end.x - start.x) == 1 || end.y - start.y == 1)
	{
		cout << img[start.x][start.y];
		return;
	}

	//이미지의 데이터를 확인한다.
	int check = img[start.x][start.y];
	for(int i = start.x; i < end.x; i++)
	{
		for(int j = start.y; j < end.y; j++)
		{
			//데이터가 서로 다르면 다른 값으로 압축해야 한다.
			if(check != img[i][j])
			{
				cout << '(';

				coord mid = getMid(start, end);
				solve(start, mid);
				solve({ start.x, mid.y }, { mid.x, end.y });
				solve({ mid.x, start.y }, { end.x, mid.y });
				solve(mid, end);

				cout << ')';
				return;
			}
		}
	}

	cout << check;
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);

	int N;
	cin >> N;

	for(int i = 0; i < N; i++)
	{
		string s;
		cin >> s;
		for(int j = 0; j < N; j++)
		{
			img[i][j] = s[j] - '0';
		}
	}

	solve({ 0, 0 }, { N, N });
}