(백준/C++) 2293_동전 1

2293번: 동전 1 (acmicpc.net) 문제는 n가지 종류의 동전으로 k원의 가치를 만드는 동적 계획법(Dynamic Programming, DP) 문제입니다.

동적 계획법(Dynamic Programming, DP)이란, 큰 문제를 작은 문제들로 나누어 풀어나가고 작은 문제의 해를 저장해 다시 계산하지 않고 사용하는 방식입니다.

이 문제에서 주어지는 조건은 다음과 같습니다.

1. 각각의 동전은 몇 개라도 사용할 수 있다. 즉, 한 가지의 동전을 여러번 사용할 수 있습니다.
2. 사용한 동전의 구성이 같은데, 순서만 다른 것은 같은 경우이다. ([1, 1, 2]나 [2, 1, 1]이나 같은 경우의 수로 봅니다.)

---

접근법

우선, 이 문제는 n가지 종류의 동전이 있고, 이 동전들을 사용하여 k원을 만들 수 있는 경우의 수를 계산하는 문제입니다.

저는 k원을 만들 수 있는 경우를 저장하는 동적 계획법을 세웠습니다.

이때, dp[k]부터 차근차근 계산해 나아가는 방법도 있을 수 있지만, n번째 동전으로 각 가치를 만드는 경우의 수를 계산하는 방법이 더 쉽습니다.

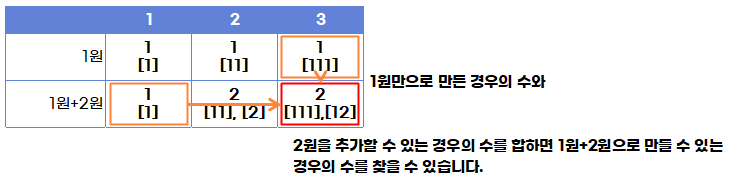
즉, 1원으로 각 가치를 만들 수 있는 경우의 수를 더해갑니다.

예를 들어, 1원짜리 동전으로 2원을 만드는 방법 1가지, 3원을 만드는 방법 1가지 등이 저장됩니다.

그리고 2원으로 각 가치를 만들때, k=4인 경우의 수는 k=2원을 만드는 경우의 수만큼 존재합니다.

무슨 말이냐면, k=2원을 만들 수 있는 경우의 수가 1원으로 만든 1가지 경우의 수와 2원으로 만든 1가지 경우의 수를 합쳐 2가지라고 본다면, k=4원을 만들 수 있는 경우의 수도 [1, 1, 2], [2, 2]로 2가지이기 때문입니다. (문제에서 주어지는 조건에서 순서만 다른 것은 같은 경우라고 했으니 [1, 1, 2]나 [2, 1, 1]이나 같은 경우로 봐야하기 때문입니다.)

이것과 비슷한 문제는 1904번: 01타일 (acmicpc.net) 문제입니다.

1) Tabulation(Bottom-up) 방식

따라서, dp[k] 배열을 정의해서 k원을 만들 수 있는 경우의 수를 계산할 때, 작은 경우부터 순서대로 값을 만들어 갔습니다.

부분 문제로 나누기

각 동전을 사용하여 만들 수 있는 금액의 경우의 수를 만들어 가야 합니다.

이때, 초기에 dp[0] = 1로 설정합니다. 그래야 점화식을 사용해서 경우의 수를 더해가기 편합니다. (또한, 0원을 만들 수 있는 경우의 수는 동전을 하나도 쓰지 않은 경우 1개로 볼 수도 있습니다.)

예를 들어, 동전 1원을 이용해 가치 1원을 만드는 경우의 수는 1원을 추가할 수 있는(1원을 추가해서 가치 1원을 만들 수 있는) 경우의 수인 0원의 경우의 수를 가져와야 하기 때문입니다.

중복된 부분 문제

동전을 하나씩 사용해보면서 k원을 만들 수 있는 경우의 수를 계산할 때, 이전에 계산한 $dp[i - coin]$의 값을 재활용합니다.

2) 점화식 찾기

따라서, 이를 사용한 점화식을 다음과 같이 정의할 수 있습니다.

\[dp[v]=dp[v]+dp[v-coin]\]

여기서 coin은 현재 사용할 동전의 금액입니다. ($dp[v]$는 이전 동전들을 사용해서 찾은 v원을 만들 수 있는 경우의 수입니다.)

풀이

#include <iostream>
#include <vector>
using namespace std;

int solve(const vector<int>& coins, const int target)
{
	vector<int> dp(target + 1, 0);
	dp[0] = 1; // 0원을 만들 수 있는 경우의 수를 1가지로 가정합니다.

	// 동전을 한 종류씩 사용하면서 계산합니다.
	for (const int& coin : coins)
	{
		// 현재 동전으로 만들 수 있는 경우의 수를 더해나갑니다.
		for (int v = coin; v <= target; v++)
		{
			if (v - coin >= 0)
				dp[v] += dp[v - coin]; // 현재 동전을 사용하지 않은 경우의 수 + 현재 동전을 사용하면 만들어지는 경우의 수
		}
	}

	return dp[target];
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);

	int N, K;
	cin >> N >> K;

	vector<int> coins(N);
	for(int i = 0; i < N; i++)
		cin >> coins[i];

	cout << solve(coins, K);
}