(백준/C++) 2805_나무 자르기

2805번: 나무 자르기 (acmicpc.net) 문제는 이진 탐색(Binary search) 문제 중 파라메트릭 서치(Parametric search) 문제입니다.

Parametric Search란?

Parametric search는 이진 탐색(binary search)의 변형 중 하나로, 주로 최적화 문제를 결정 문제로 변환해 푸는 데 사용됩니다.

이 방식은 문제의 정답이 특정 범위 내에서 연속적인 값을 가질 때 유용합니다.

여기에서 결정 문제란, “예”, “아니오”로 답을 찾는 방식의 문제를 말합니다.

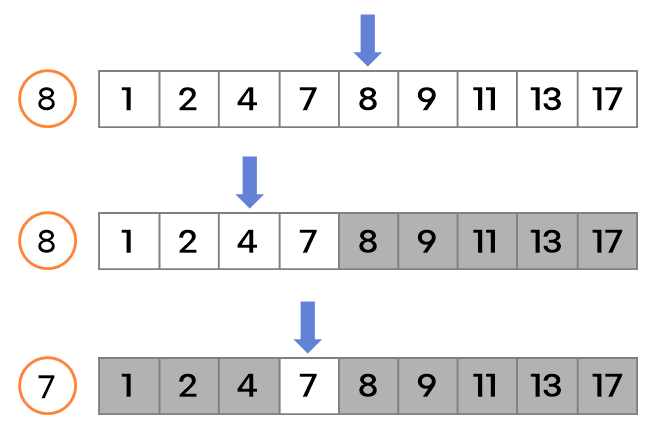
예를 들어, “5보다 큰 수 중 5에 가까운 수는?”을 주어진 배열에서 $N$번 수행하지 않고 이진 탐색을 통해 $logN$번 수행하는 문제로 바꿀 수 있습니다.

즉, 기존의 이진 탐색(binary search)이 특정 값을 찾기 위한 이진 탐색이라면, Parametric search는 특정 문제를 해결하기 위한 이진 탐색이라고 볼 수도 있을 것 같습니다.

---

접근법

2805번: 나무 자르기 (acmicpc.net) 문제는 N개의 나무가 주어졌을 때, 필요한 길이 M을 만들기 위한 최적의 절단기 높이 H를 구하는 문제입니다.

이때, 주의해야 할 점은 절단기의 높이 H를 더해야 하는게 아니라, 절단기의 높이 H로 자른 나머지 길이를 합해서 최대한 M에 가깝게 만들어야 하는 것이라는 점입니다.

1) 범위 설정

이 문제는 Parametric Search를 사용하여 풀 수 있습니다. 절단기의 최소 길이는 1, 최대 길이는 주어진 나무 중 가장 긴 것으로 범위를 잡고 이진 탐색을 하면 됩니다.

2) 결정 함수 설정

결정 함수란, 이진 탐색을 진행하면서 결과를 결정하기 위한 함수입니다.

이 문제에서는 절단기의 높이 H로 모든 나무를 자르고 남은 나머지 길이를 합한 길이가 됩니다.

이 결과 값을 통해 이진 탐색의 오른쪽으로 탐색할지, 왼쪽으로 탐색할지 결정합니다.

3) 이진 탐색

범위를 잡았다면, 중간 값부터 시작합니다.

• 나무의 길이가 부족하다면: 현재 절단기의 높이가 높게 설정되어있기 때문에 왼쪽으로 이진 탐색을 합니다.
• 나무의 길이가 넘는다면: 필요한 나무의 길이를 넘어섰지만, 최적의 값을 찾기 위해 오른쪽으로 이진 탐색을 합니다.

이렇게 이진 탐색의 범위를 좁혀가며 탐색해 가다보면 최적의 답을 찾을 수 있는 방식이 Parametric search 입니다.

---

풀이

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

// 최소한의 길이로 만족할 수 있는 길이를 찾아야 한다.
long long cuttingLog(const vector<int>& Logs, int height)
{
	long long result = 0;
	for (const int& log : Logs)
		if (log > height) result += (log - height);

	return result;
}

int findLength(const vector<int>& Logs, int need)
{
	int min = 1, max = *max_element(Logs.begin(), Logs.end());
	int result = 0;

	while(min <= max)
	{
		int mid = (min + max) / 2; // 통나무의 높이를 설정한다.
		long long tmp = cuttingLog(Logs, mid);

		if(tmp < need)
		{
			max = mid - 1; // mid로 자른 길이가 원하는 길이가 안되는 경우 왼쪽으로 이진 탐색을 한다.
		}
		else
		{
			result = mid;
			min = mid + 1; // mid로 자른 길이가 원하는 길이를 넘는 경우 오른쪽으로 이진 탐색을 한다.
		}
	}
	return result;
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);

	int N, H;
	cin >> N >> H;

	vector<int> Logs(N);
	for (int i = 0; i < N; i++)
		cin >> Logs[i];

	cout << findLength(Logs, H);
}