(백준/C++) 6549_히스토그램에서 가장 큰 직사각형

히스토그램이란, 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형으로, 6549번: 히스토그램에서 가장 큰 직사각형 (acmicpc.net) 문제에서는 이 히스토그램에서 가장 넓이가 큰 직사각형을 분할 정복으로 구하는 방법을 물어보고 있습니다.

분할 정복(Divide and Conquer)이란, 큰 문제를 작은 부분 문제로 나누어 해결하고, 그 결과를 합쳐 원래 문제의 해결책을 찾는 방법입니다.

즉, 이 히스토그램을 분할해서, 문제를 풀어내고, 결과를 가지고 최종 해를 구하면 됩니다.

---

접근법

분할 정복에서의 가장 간단한 방법은, 큰 문제를 N개로 나누는 것입니다.

저는 이 문제를 각 단계에서 2개로 나누고, 각 문제를 분할하여 푼 다음에 결합하여 풀지 못한 문제를 푸는 방식으로 접근했습니다.

결합 단계에서는 중간 지점(나눈 부분)부터 시작해서 각 영역으로 확장해 가면서 가장 큰 직사각형을 저장하는 형식으로 풀었습니다.

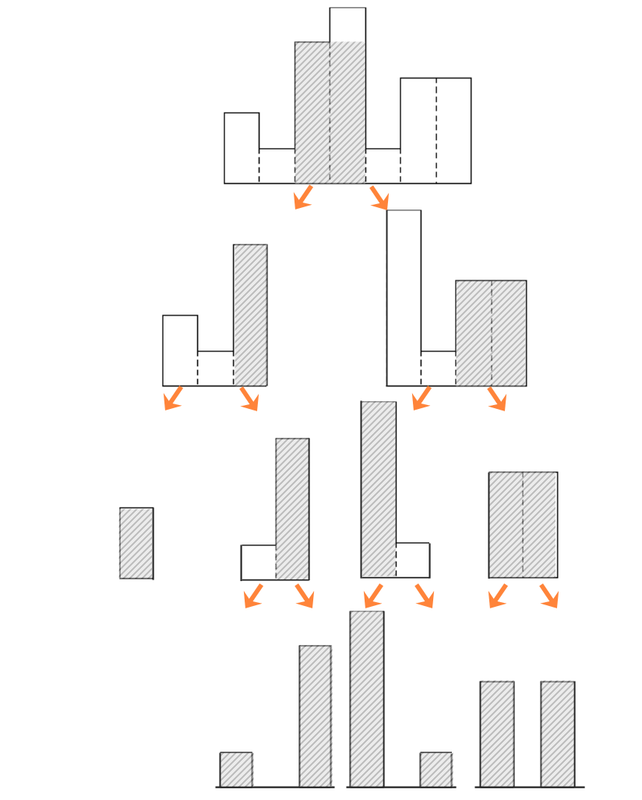
그림으로 표현하면 아래와 같습니다.

분할 - 정복 - 결합 단계로 나눠보면 다음과 같습니다.

1) 분할(Divide)

히스토그램을 좌·우 두 부분으로 나눕니다.

2) 정복(Conquer)

나눠진 각 부분에 대해 가장 큰 직사각형을 찾습니다. 즉, 나눠진 각 부분에 대해 재귀적으로 문제를 해결하면서, 각 부분에서 나온 결과 중 큰 직사각형의 넓이를 사용합니다.

기저 사례(Base Case): 영역이 한 칸인 경우 현재 칸의 넓이를 사용합니다.

3) 결합(Combine)

나눠질 때, 계산되지 않은 부분인 “중앙을 포함하는 직사각형”의 넓이 중 가장 큰 넓이를 찾습니다.

이후, 정복 단계에서 찾은 해와 결합 단계에서 찾은 해 중에서 가장 큰 직사각형의 넓이를 사용합니다.

---

풀이

이 문제에서 가장 고민 되는 부분이 결합 단계에서의 가장 큰 직사각형을 찾는 부분일 것입니다.

단순히 결합 단계에서 중앙에서 시작해 양 쪽 끝까지 탐색하는 방법도 있겠지만, 결합된 크기만큼만 검사하는 방법을 사용했습니다.

이때, 중앙에서 시작해 양 쪽 중에서 값이 큰 방향으로 먼저 확장해야, 가장 큰 넓이의 직사각형을 찾을 수 있습니다.

#include <iostream>
#include <vector>
using namespace std;

long long solve(const vector<int>& arr, int s, int e)
{
	// 기저사례: 하나의 직사각형의 크기
	if (s == e - 1) return arr[s];

	// 분할: 두 개의 부분으로 나눈다.
	int m = (s + e) / 2;

	// 정복: 두 부분 중 큰 사각형을 찾는다.
	long long result = max(solve(arr, s, m), solve(arr, m, e));

	// 결합: 두 부분을 결합한 후, 중앙에서 시작한 직사각형의 넓이 중 최대값을 찾는다.
	int l = m, r = m;
	long long height = arr[m];
	while(r - l < e - s)
	{
		// 경계까지 확장
		long long lp = s < l ? arr[l - 1] : -1;
		long long rp = r < e ? arr[r] : -1;

		// 좀 더 큰 영역으로 확장
		if(lp >= rp)
		{
			height = min(height, lp);
			l--;
		}
		else
		{
			height = min(height, rp);
			r++;
		}

		result = max(result, height * (r - l));
	}

	return result;
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);

	int N;
	while (true)
	{
		cin >> N;
		if (!N) return 0;

		vector<int> nums(N, 0);

		for(int i = 0; i < N; i++)
		{
			cin >> nums[i];
		}

		cout << solve(nums, 0, N) << '\n';
	}
}