(백준/C++) 9251_LCS(Longest Common Subsequence, 최장 공통 부분 수열)

LCS (Longest Common Subsequence, 최장 공통 부분 수열)은 두 개의 문자열에서 공통으로 나타나는 가장 긴 부분 수열을 찾는 동적 프로그래밍 알고리즘입니다.

이 알고리즘은 DNA 서열 분석부터 데이터 압축까지 다양한 응용 분야에서 사용할 수 있는 매우 중요한 알고리즘입니다.

하지만, 이 문제를 처음 접하게 되면 풀이 방법을 찾기 어려울 수 있습니다.

9251번: LCS 문제 바로가기

동적 계획법(Dynamic Programming, DP)이란, 큰 문제를 작은 문제들로 나누어 풀어나가고 작은 문제의 해를 저장해 다시 계산하지 않고 사용하는 방식입니다.

우선, 동적 계획법 문제는 최적 부분 구조와 중복된 부분 문제의 두 가지 속성을 가집니다. 이 문제도 최적 부분 구조와 중복된 부분 문제에 대해 먼저 생각해보겠습니다.

1. 최적 부분 구조: LCS 문제에서는 두 문자열의 부분 문자열 간의 LCS를 구하고 결합하여 더 큰 부분 문자열의 LCS를 구하는 식으로 최적 부분 구조라고 할 수 있습니다.
   예를 들어, ACAYKP와 CAPCAK라는 두 문자열의 LCS를 구하려면 다음과 같이 작은 부분 문제부터 시작할 수 있습니다.
   AC와 CA의 LCS, ACAY와 CAPC의 LCS, ACAYK와 CAPCAK의 LCS, ⋯ 이러한 부분 문제의 최적 해결책을 결합해 가면서 전체 문자열의 LCS를 구할 수 있습니다.
2. 중복된 부분 문제: 이 문제에서는 동일한 부분 문자열 간의 LCS를 여러 번 계산해야 할 수 있습니다.
   예를 들어, ACAYKP와 CAPCAK의 LCS를 구하는 과정에서 AC와 CA의 LCS를 여러 번 계산해야 할 수 있습니다.

---

접근법

이 문제는 두 문자열의 공통 부분중에 가장 긴 공통 부분 수열을 구하는 문제입니다.

A가 CAPCAK라는 문자열 중에서 공통되는 가장 긴 부분 수열은 A에서 시작하는 A입니다. AC가 CAPCAK라는 문자열 중에서 공통되는 가장 긴 부분 수열은 A가 있고 다음에 C가 있는지 확인해서 기존 구한 해에서 최적해를 구할 수 있습니다.

2차원 배열 사용

이런 방식으로 구현하기 위해서는 두 문자열의 각 문자를 요소로 가진 2차원 배열을 사용할 수 있습니다.

이제 이 2차원 배열에는 첫 번째 문자열의 첫 i글자와 두 번째 문자열의 첫 j글자 사이의 LCS의 길이가 저장 될 것입니다.

이제 각 배열의 위치에 LCS의 길이를 계산하고, 이전에 계산된 길이를 가지고 다음 LCS의 길이를 계산하는 식으로 나아가면 되겠습니다.

---

풀이

최장 공통 부분 수열의 핵심은 두 문자열을 비교하는 과정에서 중간에 다른 문자열이 끼어있더라도 다음에 공통된 부분이 나오면 카운트가 증가한다는 점입니다.

즉, 공통된 부분 이후에도 그 값을 사용해야 하므로 어디에 있던 앞에서 계산된 LCS 값이 유지되어야 합니다.

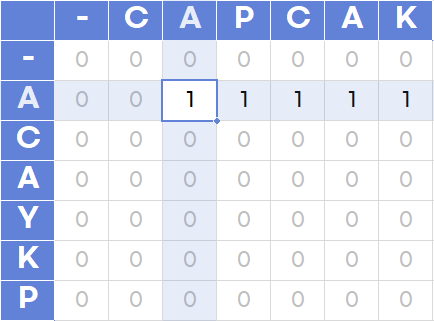
1. 배열 초기화와 공통 부분 찾기

LCS는 2차원 배열로 문자열의 각 문자를 저장하고 공통된 부분이 나타나면 [i-1][j-1]에 저장된 길이에서 1을 증가시켜 줍니다.

여기에서 [i-1][j-1]의 의미는 두 문자열의 공통된 문자의 바로 앞 부분을 의미합니다.

예를 들어, 아래에서 A를 CAPCAK에 대해 검사하고 있는데, A와 P에서의 1은 ‘A’와 ‘CAP’ 문자의 LCS 길이입니다. 따라서 ‘A’와 ‘CA’로 서로 공통된 부분에서의 길이를 증가시키려면 두 문자의 바로 앞인 ‘-’와 ‘C’까지 검사한 LCS의 길이에 1을 더하는 것입니다.

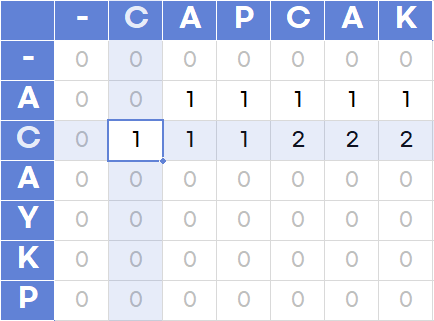
2. AC와 CAPCAK의 LCS 찾기

1과 같은 방식으로 공통된 부분을 찾습니다.

이때, 공통된 부분이 나타나면 [i-1][j-1]에 저장된 길이에서 1을 증가시켜 주고,

공통된 부분이 없다면 [i-1][j]나 [i][j-1]의 LCS 길이를 그대로 따라가야 합니다.

그 이유는 위에서 언급했듯이 중간에 다른 문자열이 끼어있더라도 다음에 공통된 부분이 나오면 카운트가 증가하기 때문입니다.

이걸 저장해 둬야 같은 문자가 나중에 나타나더라도 [i-1][j-1]에 최대 LCS 길이가 저장되어 있을 수 있습니다.

이때, [i-1][j]나 [i][j-1]의 max를 사용해야 하는데, 이는 두 문자열 양쪽에서의 LCS 길이를 유지해야 하기 때문입니다.

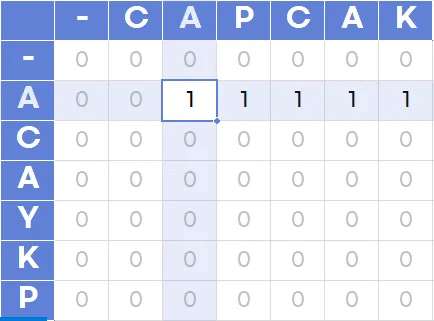
3. 이제 위 과정을 반복합니다.

공통된 부분이 나타나면 [i-1][j-1]에 저장된 길이에서 1을 증가시켜 주고,

공통된 부분이 없다면 [i-1][j]나 [i][j-1]의 LCS 길이를 그대로 따라가다보면 마지막 위치에 결국 LCS의 최대 길이가 저장되게 됩니다.

이는 “CAPCAK”로 “ACAYKP”를 비교하는 것과 “ACAYKP”로 “CAPCAK”를 비교하는 공통된 LCS의 최대 길이를 뜻합니다.

---

#include <iostream>
#include <vector>
using namespace std;

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);

    string str1, str2;
    cin >> str1 >> str2;

    int len1 = str1.size() + 1;
    int len2 = str2.size() + 1;

    vector<vector<int>> table(len1, vector<int>(len2, 0));

    // LCS 알고리즘 구현
    for (int i = 1; i < len1; i++) 
    {
        for (int j = 1; j < len2; j++) 
        {
            if (str1[i - 1] == str2[j - 1]) 
            {
                // 문자가 같으면 (i-1, j-1)의 값에 1을 더함
                table[i][j] = table[i - 1][j - 1] + 1;
            }
            else 
            {
                // 문자가 다르면 (i, j-1)과 (i-1, j) 중 큰 값을 유지
                table[i][j] = max(table[i - 1][j], table[i][j - 1]);
            }
        }
    }

    cout << table[len1 - 1][len2 - 1];
}