빅오(Big-O) 표기법
빅 오(big-O) 표기법이란, 알고리즘의 효율성을 표현하기 위한 표기법입니다.
빅 오 표기법 같은 표기법을 점근적 표기법이라고 하는데, 알고리즘의 성능을 입력 값의 크기가 커질 때, 어떻게 변하는지. 즉, 성능의 성장률을 수학적으로 표현하는 방법입니다. (데이터의 수에 따라 성능에 영향을 미치는 값의 크기를 수학적으로 표현)
즉, 알고리즘 내의 성능을 그래프로 그리는 대신 간략하게 표기하여 한눈에 알아보기 쉽도록 표기하는 방법입니다.
(이 표기법을 공부하기 전 지수와 로그에 대한 지식이 있어야 이해하기 편합니다.)
여러가지 점근적 표기법
Big-Ω (빅 오메가)
Big-Ω 표기법은 알고리즘의 점근적 하한선을 나타내는 데 사용됩니다.
즉, 알고리즘 성능의 최소한의 성능을 나타내는 것으로, 알고리즘이 어떤 크기의 입력에 대해서도 최소한 얼마나 많은 시간이나 최소한의 공간이 필요한지를 나타냅니다.
시간 복잡도에 대해서는 최상의 실행 시간을 표기한다고도 합니다. 하지만 공간 복잡도의 입장에서 보면 알고리즘을 실행하는데 필요한 최소한의 공간을 표기합니다.
예를 들어, 이진 탐색의 공간 복잡도는 포인터를 사용하면 공간이 별로 필요 업기 때문에 Ω(1)의 효율을 보이며, 수행 시간의 경우 중앙에 답이 있는 경우 Ω(1)이 될 수 있습니다.
하지만, 삽입 정렬과 같은 경우에는 배열의 처음부터 끝까지 탐색해야 하기 때문에 시간 복잡도는 Ω(n)이 최소한으로 필요합니다.
Big-θ (빅 세타)
Big-θ 표기법 알고리즘의 상한과 하한 모두를 고려하여, 평균을 표기한다.
Big-O (빅 오)
Big-O 표기법은 알고리즘의 점근적 상한선을 표기합니다.
주로 사용되는 표기법으로, 일반적으로 고려되어야 하는 성능을 표현하게 됩니다.
빅 세타의 경우에는 계산이 복잡해지기 때문에, 주로 최악의 경우 필요한 성능을 예측할 수 있습니다.
빅오 표기법(big-O) 특징
이 글에서는 주로 사용하는 big-O 표기법에 대해서만 다룰 예정입니다.
big-O 표기법은 알고리즘 성능에 미미한 영향을 주는 것들은 무시하고 간략하게 표시합니다.
1. 상수항만 존재하는 경우 1로 표시한다.
big-O 표기법의 성능이 상수항만 존재하는 경우에는 1로 표시합니다.
점근적 표기법에서는 상수의 경우 성장을 표시하지 않기 때문에 1로 표기합니다. (1이나 9나 그래프에서 입력 값의 크기와 상관없이 일정한 그래프를 표시하기 때문에)
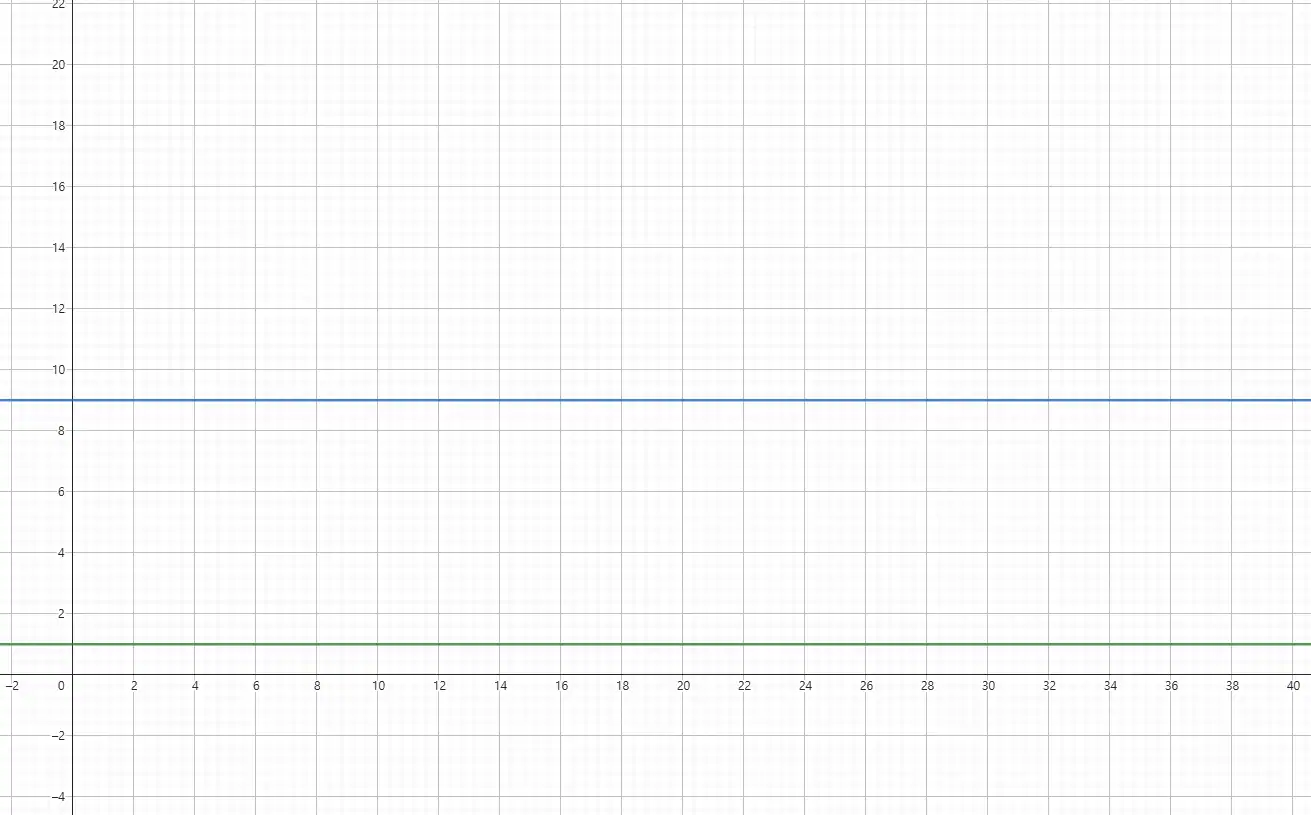 그래프를 무한히 축소하면, 각 상수항의 영향력은 상대적으로 중요하지 않게 되거나 무시할 수 있다.
그래프를 무한히 축소하면, 각 상수항의 영향력은 상대적으로 중요하지 않게 되거나 무시할 수 있다.
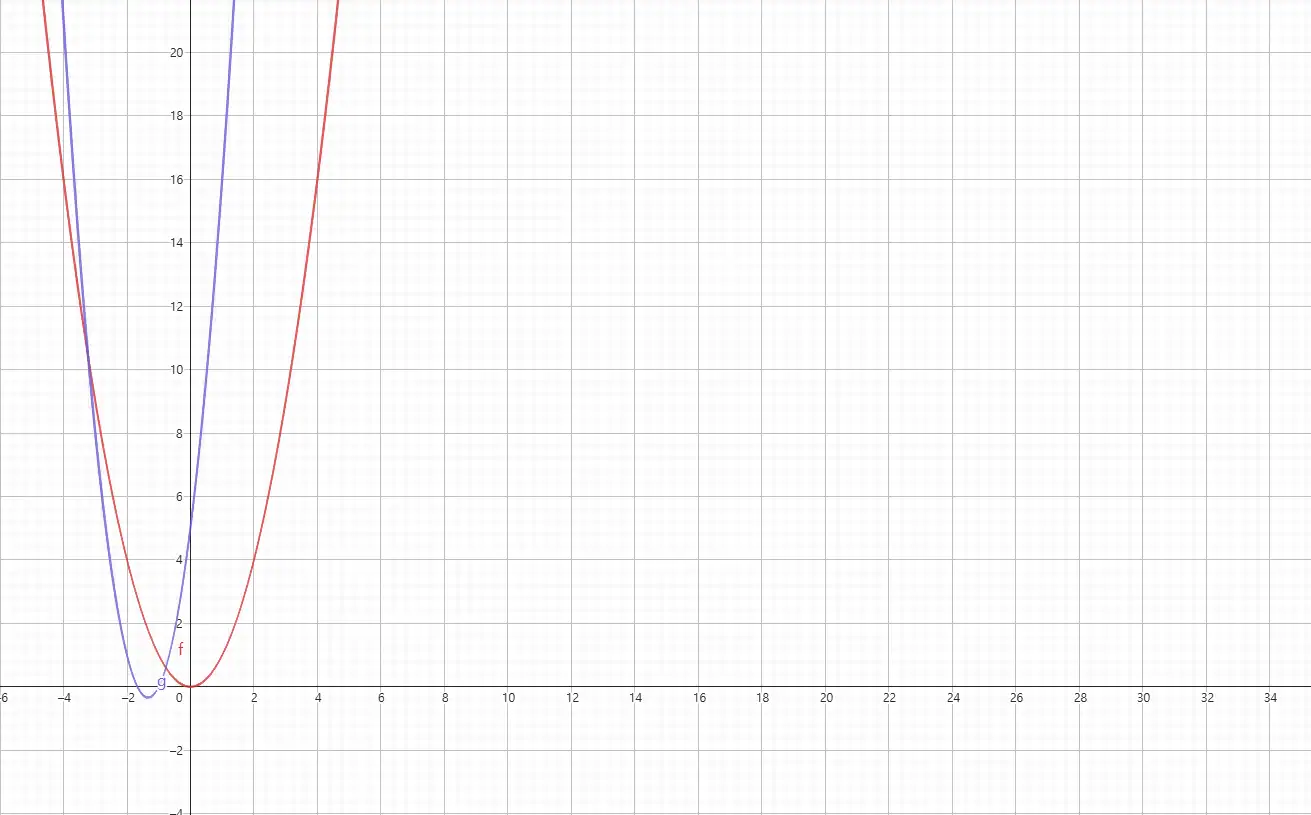
2. 상수항과 계수를 무시한다.
따라서 1번과 같은 의미로 각 수식의 상수항이나 계수도 무시할 수 있습니다.
즉, $O(3N+5)$를 $O(N)$으로 표현합니다.
단, 상수항만 있는 경우, 1. 상수항만 존재하는 겨우 1로 표시한다는 법칙에 따라 1로 표시됩니다.
3. 최고차항만 표기한다.
위와 같은 의미로 $O(3N^2+8N+5)$ 또한 $O(N^2)$으로 표현합니다.
빅오 표기법(big-O) 수식 비교
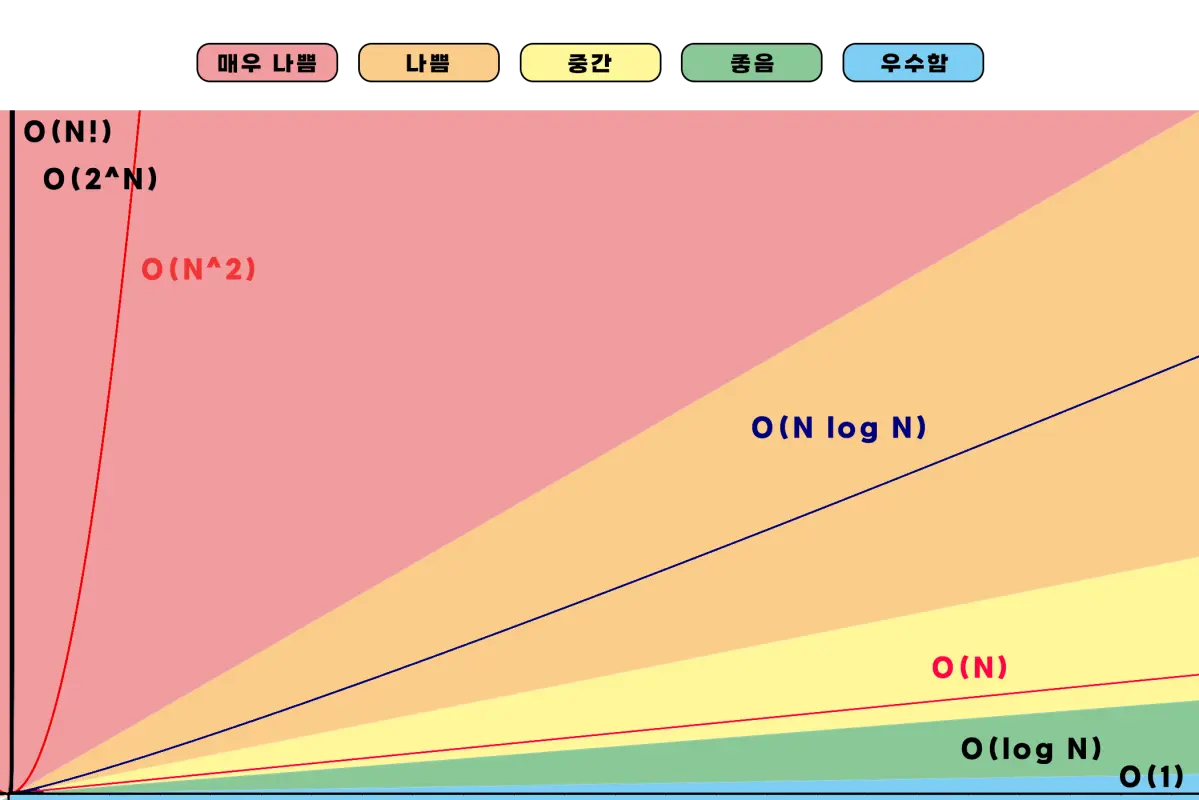
위와 같은 특징을 적용하여 알고리즘 효율을 수식으로 표현하면 대부분 아래와 같은 표기법으로 표현할 수 있습니다.
\[O(1) < O(log N) < O(N) < O(N log N) < O(N^2) < O(2^N)<O(N!)\]