우선순위 큐(Priority Queue)와 힙(Heap)

• 라이브러리
  • C++: <queue>, std::priority_queue<T>
  • C#: System.Collections.Generic, PriorityQueue<T, P>
  • JAVA: java.util, PriorityQueue<E>
  • Python: import heapq, from queue import PriorityQueue
• 탐색 시간: $O(1)$
• 요소 추가/삭제: $O(log N)$

우선순위 큐(Priority Queue)

우선순위 큐는 각 요소가 우선순위를 갖고 있으며, 우선순위가 높은 요소가 먼저 처리되는 큐입니다.

즉, 순서를 보장하는 형태의 큐(Queue)지만, 우선순위를 가지고 있는 큐이기 때문에 우선순위 큐(Priority Queue)라는 이름이 붙었습니다.

따라서, 큐와 달리 우선순위 큐에서는, FIFO(First In, First Out) 원칙이 아닌 요소의 우선순위에 따라 요소가 큐에서 제거됩니다.

우선순위 큐는 여러 방식으로 구현할 수 있겠지만, 일반적으로 힙(Heap) 자료구조를 사용하여 구현됩니다.

힙(Heap)

힙(Heap)은 완전 이진 트리(Complete Binary Tree) 의 일종으로, 특정한 조건을 만족하는 트리 구조입니다.

힙은 크게 최대 힙(Max Heap)과 최소 힙(Min Heap)으로 나눌 수 있습니다.

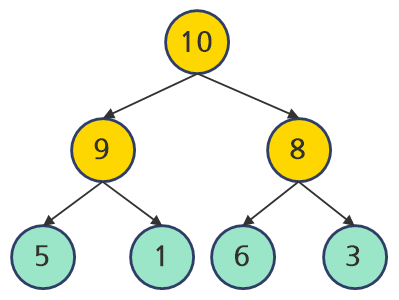
최대 힙(Max Heap)

부모 노드의 값이 자식 노드의 값보다 항상 크거나 같습니다. 루트 노드에는 가장 큰 값이 위치하게 됩니다.

형제 노드 사이에는 정렬이 되지 않습니다.

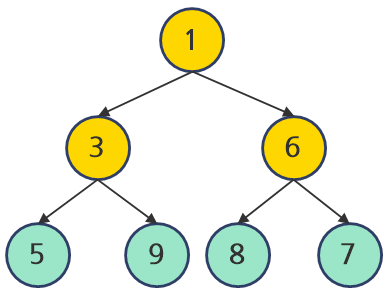
최소 힙(Min Heap)

부모 노드의 값이 자식 노드의 값보다 항상 작거나 같습니다. 루트 노드에는 가장 작은 값이 위치하게 됩니다.

형제 노드 사이에는 정렬이 되지 않습니다.

힙의 주요 연산

1. 삽입(Insertion): 새로운 원소를 힙에 추가합니다. $O(log N)$
   • 새로운 원소를 완전 이진 트리의 마지막 위치에 삽입합니다.
   • 삽입된 원소를 적절한 위치로 이동시키며 힙 속성을 유지합니다. (상향 조정, bubble-up)
2. 삭제(Deletion): 보통 루트 노드를 삭제하는 연산입니다. $O(log N)$
   • 루트 노드를 삭제하고, 마지막 노드를 루트 위치로 이동시킵니다.
   • 이동된 노드를 적절한 위치로 이동시키며 힙 속성을 유지합니다. (하향 조정, bubble-down)
3. 힙 만들기(Heapify): 주어진 배열을 힙 구조로 변환하는 연산입니다. $O(N)$
   • 상향식 방법을 사용하여 배열의 중간부터 시작하여 각 노드에 대해 하향 조정을 반복합니다.

힙의 용도

• 우선순위 큐: 다익스트라 알고리즘, 작업 스케줄링 등에서 사용됩니다.
• 힙 정렬(Heap Sort): 효율적인 정렬 알고리즘 중 하나로 사용됩니다.

배열에서 힙의 구현

힙은 배열로도 구현할 수 있습니다.

배열을 사용하게 되면 부모와 자식 노드 간의 관계를 인덱스로 쉽게 표현할 수 있습니다.

• 부모 노드: 인덱스 $i$의 부모 노드 인덱스는 $(i - 1) / 2$
• 왼쪽 자식 노드: 인덱스 $i$의 왼쪽 자식 노드 인덱스는 $(2 * i) + 1$
• 오른쪽 자식 노드: 인덱스 $i$의 오른쪽 자식 노드 인덱스는 $(2 * i) + 2$

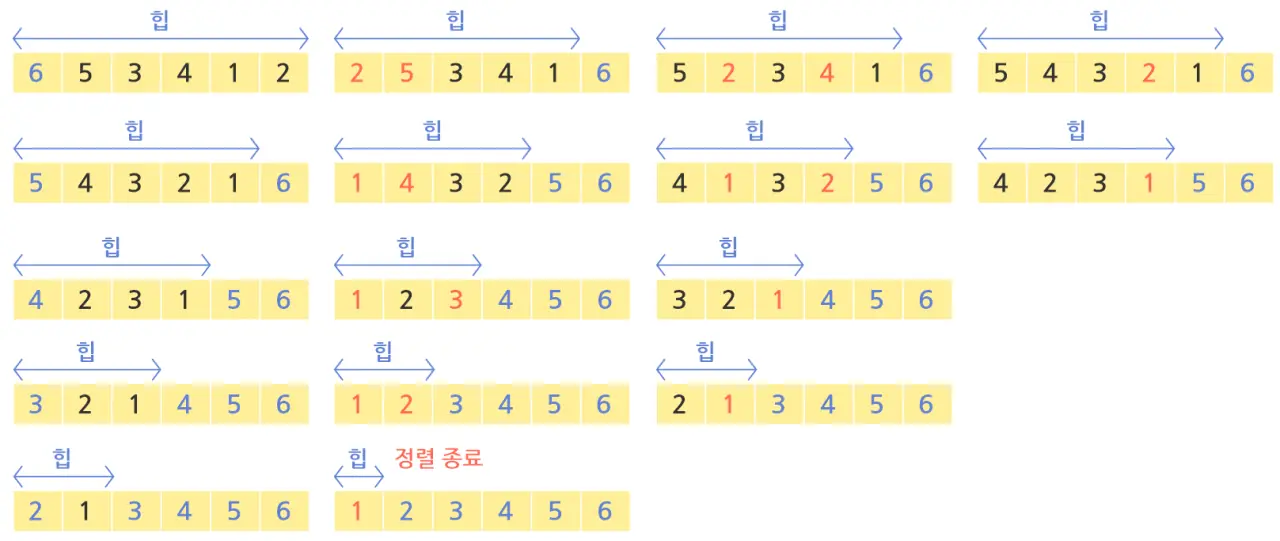
힙 정렬

힙 정렬은 힙의 속성을 이용해서 정렬을 하는 방법입니다.

• 평균 시간 복잡도: $O(NlogN)$
• 최악 시간 복잡도: $O(NlogN)$
• 공간 복잡도: $O(1)$

1. 입력된 값들로 최대 힙을 만듭니다. 이 작업은 힙 만들기(Heapify) 작업으로 $O(N)$의 시간이 걸립니다.
2. 힙에서 최댓값을 꺼내 힙의 끝 부분에 저장하는 힙 삭제 과정을 진행합니다. (heap[size-1]위치에 저장)
3. 힙의 크기를 1 줄이고 제자리가 아닌 원소(힙 속성이 적용되지 않은 원소)로 힙 속성을 복원합니다.
4. 힙에 원소가 1개 남을 때까지 ‘2~3’과정을 반복합니다.