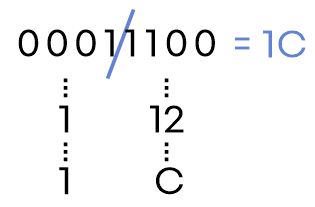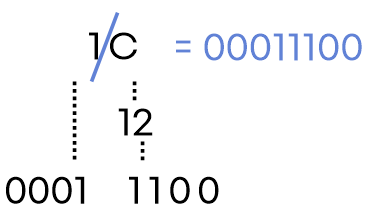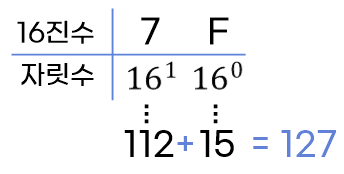진법과 진법 변환(2진법, 8진법, 16진법)

진법 표

진법
2진법	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
8진법	0	1	2	3	4	5	6	7
10진법	0	1	2	3	4	5	6	7	8	9
16진법	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

2진법(Binary)

2진법은 숫자를 0과 1, 두 가지 숫자로 표현하는 방식입니다.

컴퓨터와 같은 전자기기는 전기 신호로 데이터를 표현/저장 할 수 있습니다.
따라서, 2진법은 컴퓨터가 전기적으로 ‘켜짐’(1)과 ‘꺼짐’(0) 상태라고 이해하셔도 좋을 것 같습니다.

특징

• 표기: 컴퓨터에서는 0b로 시작해서 표현합니다. (예: 0b1010)
• 비트(bit): 2진법의 각 자리수를 비트라고 합니다.

8진법(Octal)

8진법은 숫자를 0부터 7까지 총 여덟 가지 숫자로 표현하는 방법입니다.

평소에는 쓸 일이 없는 진법이지만, 2진법으로 변환 시 2진법의 세 비트를 묶어서 표현할 수 있습니다. (7을 나타내는 이진법은 0b111)

특징

• 표기: 컴퓨터에서는 0o로 시작해서 표현합니다. (예: 0o10)
• 비트 그룹: 8진법은 2진법의 세 비트를 그룹으로 묶어서 표현할 수 있습니다.

10진법(Decimal)

10진법은 우리가 일상생활에서 사용하는 숫자 표현 방법으로, 0부터 9까지 총 열 가지 숫자로 표현합니다.

특징

• 자리 값: 각 자리의 값은 10의 거듭제곱으로 표현됩니다.

16진법(Hexadecimal)

16진법은 숫자를 0부터 9까지, 그리고 A부터 F까지의 알파벳을 사용하여 총 열여섯 가지 숫자로 표현하는 방법입니다.
A는 10, B는 11, …, F는 15를 의미합니다.

중요한 것은, 16진법은 2진법의 네 비트를 묶어서 표현할 수 있다는 점입니다.
예를들어, 16진법 ‘F’를 표현할 때, 2진법 ‘1111’로 표현합니다.

이때, 중요한 점은 1byte = 8bit 라는 점 입니다.
즉, 16bit는 16진법 두자리로 표현하고, 32bit는 16진법 네자리로 표현할 수 있다는 점입니다.

이에 따라 컴퓨터의 메모리 주소나 4bit씩 끊어서 사용될 수 있는 부분에서 빠르고 쉽게 표기할 수 있다는 점입니다.

특징

• 표기: 컴퓨터에서는 0x로 시작해서 표현합니다. (예: 0x0A)
• 비트 그룹: 16진법은 2진법의 네 비트를 그룹으로 묶어서 표현할 수 있습니다.
• 사용처: 컴퓨터 시스템과 프로그래밍에서 메모리 주소나 색상 코드 등을 표현할 때 사용됩니다.

진법 변환 방법

10진법에서 다른 진법으로 변환하기

1. 주어진 10진수를 목표하는 진법의 기수(예: 2진법은 2, 8진법은 8, 16진법은 16)로 나눕니다.
2. 나머지를 기록하고, 몫을 다시 같은 기수로 나눕니다.
3. 이 과정을 몫이 0이 될 때까지 반복하고, 나머지를 역순으로 배열하여 최종 결과를 얻습니다.

2진법에서 8진법이나 16진법으로 변환하기

1. 2진수를 오른쪽에서 왼쪽으로 3자리(8진법) 또는 4자리(16진법)씩 그룹화합니다.
2. 각 그룹을 해당하는 8진수나 16진수로 변환합니다. (바로 변환하기 어려운 경우 10진법으로 변환 후 변환합니다.)

8진법이나 16진법에서 2진법으로 변환하기

1. 각 8진수나 16진수 숫자를 해당하는 2진수 그룹으로 변환합니다. 예를 들어, 8진법에서는 각 숫자를 3자리 2진수로, 16진법에서는 각 숫자를 4자리 2진수로 변환합니다. (바로 변환하기 어려운 경우 10진법으로 변환 후 변환합니다.)

다른 진법에서 10진법으로 변환하기

1. 각 자릿수를 해당 진법의 거듭제곱에 대응하는 10진수의 값으로 변환하고, 이를 모두 더합니다.