해시 테이블(Hash Table)과 개방 주소법(Open Addressing), 체이닝(Chaining)
- 탐색 시간
- 평균: $O(1)$
- 최악: $O(N)$ (충돌 발생시)
- 요소 추가/삭제
- 평균: $O(1)$
- 최악: $O(N)$ (충돌 발생시)
해시 테이블(Hash Table)은 키(Key) 를 값(Value) 에 매핑하여 키-값 쌍을 효율적으로 저장하고 검색하는 데 사용하는 자료구조입니다.
해시 테이블은 해시 함수(Hash Function)를 사용하여 데이터를 해시 값(Hash Value)으로 변환하는 해싱(Hashing) 기법을 사용하여 데이터를 관리합니다.
해싱(Hashing)
해싱(Hashing)은 임의의 길이를 가진 데이터를 고정된 길이의 값으로 변환하는 과정입니다. 이 과정에서 사용되는 함수가 해시 함수(Hash Function)입니다.
간단한 해시 함수는 비교적 쉽게 역산할 수 있거나 충돌을 일으키기 쉬울 수 있습니다.
이렇게 변환된 해시 값은 일반적으로 사람이 읽기 어려운 형태이고 비가역적(원래 데이터로 복원 불가)입니다.
해시 함수(Hash Function)
해시 함수(Hash Function)는 임의의 길이의 입력 데이터를 받아 고정된 길이의 해시 값(Hash Value)을 반환하는 함수입니다.
모든 키에 대해 고유한 해시 값(Hash Value)을 생성하는 이상적인 해시 함수를 완전 해시 함수(Perfect Hash Function)이라고 합니다.
좋은 해시 함수의 속성
좋은 해시 함수는 다음과 같은 속성을 가집니다.
- 결정적(Deterministic): 동일한 입력 값에 대해 항상 동일한 해시 값을 반환합니다.
- 효율적(Efficient): 해시 값을 계산하는 데 걸리는 시간이 짧아야 합니다.
- 균등 분포(Uniform Distribution): 해시 값이 가능한 한 균등하게 분포되어야 합니다. 그렇지 않으면 충돌 횟수와 충돌 해결 비용이 늘어나게 됩니다.
- 충돌 최소화(Minimal Collisions): 서로 다른 입력 값들이 동일한 해시 값을 가질 확률이 낮아야 합니다.
- 원본 데이터의 민감성: 입력 데이터의 아주 작은 변화라도 해시 값에 큰 차이를 가져와야 합니다(눈사태 효과).
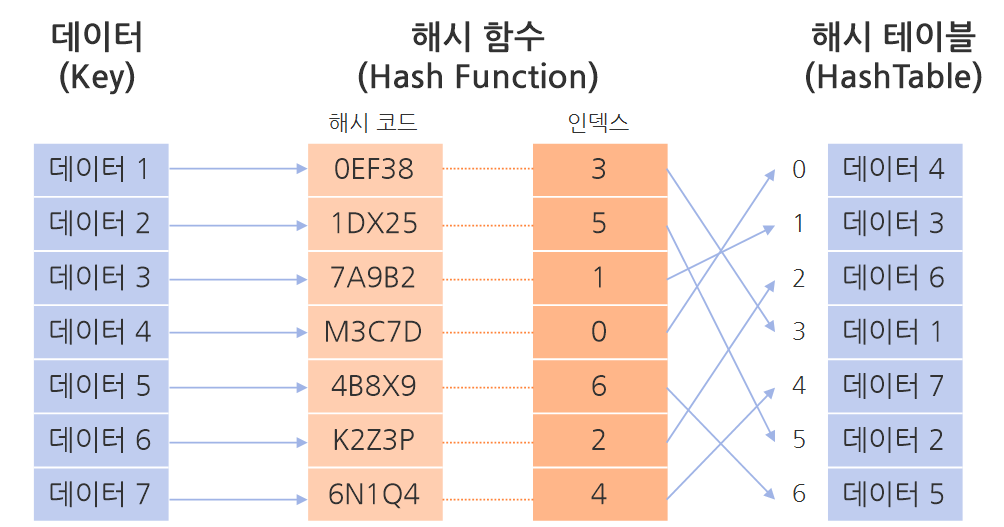
해시 테이블(Hash Table)
해시 테이블은 해시 함수를 사용하여 키(Key)를 해시 함수를 통해 고유의 값을 만들고, 이를 테이블의 인덱스(Index)로 변환하여 사용합니다.
이 해시 함수(Hash Function)의 경우, 동일한 입력 값에 대해 항상 동일한 해시 값을 반환하기 때문에 매번 같은 해시 값을 통해 접근할 수 있습니다.
따라서, 특정 키 값을 찾기 위해 해시 함수를 통해 인덱스를 구하기만 하면 되기 때문에 평균 $O(1)$의 시간으로 검색/삽입/삭제가 가능합니다.
해시 충돌
다만, 해싱의 주된 문제는 해시 충돌입니다.
해시 함수가 둘 이상의 다른 키에 대해 같은 인덱스를 생성하는 문제를 충돌(Collision)이라고 합니다.
이상적으로 해시 함수는 모든 키에 대해 고유한 주소를 반환해야 하지만, 실제로는 어떤 키 값이 들어올지 알 수 없기 때문에 불가능합니다.
해싱에서는 충돌을 다루는 많은 기법이 있는데, 이 중에서 가장 일반적인 두 방법에 대해서 알아보겠습니다.
개방 주소법(Open Addressing)
해시 충돌로 인해 동일한 주소에 다른 데이터가 있을 경우 다른 주소도 이용할 수 있게 하는 기법입니다.
즉, 충돌이 발생했을 때, 여유 공간을 찾을 때까지 차례대로 다른 주소로 이동하는 단순한 방법입니다.
개방 주소법(Open Addressing)에는 선형 탐사(Linear Probing), 제곱 탐사(Quadratic Probing), 이중 해싱(Double Hashing) 등이 있습니다.
1. 선형 탐사(Linear Probing)
선형 탐사(Linear Probing)는 가장 기본적인 충돌 해결 기법으로 해시 테이블의 빈 위치를 순차적으로 검색해 충돌을 해결하는 방법입니다.
선형탐사는 바로 인접한 인덱스에 데이터를 삽입해가기 때문에 데이터가 밀집되는 클러스터링(Clustering) 문제가 발생하고 이로인해 탐색과 삭제가 느려지게 됩니다.
클러스터링(Clustering) 문제
데이터가 해시 테이블에 삽입될 때, 연속된 주소들이 채워지기 시작하면, 새로운 데이터가 삽입될 때마다 빈 주소를 찾기 위해 더 많은 주소를 탐색해야 합니다.
또 이렇게 연속된 주소들이 채워져 하나의 큰 클러스터를 형성하게 되면, 새로운 데이터를 삽입하거나 기존 데이터를 검색할 때 클러스터를 탐색하는 데 많은 시간이 소요됩니다.
즉, 클러스터가 커지면 해시 테이블의 평균 검색 시간과 삽입 시간이 증가하게 되어, 해시 테이블의 효율성이 크게 저하됩니다.
2. 제곱 탐사(Quadratic Probing)
제곱 탐사(Quadratic Probing)는 선형 탐사의 클러스터링 문제를 완화하는 방법으로, 빈 위치의 검색 인덱스를 제곱으로 늘려 검색하는 방식입니다.
$1^2$,$2^2$,$3^2$… 형태로 탐색하기 때문에 선형 탐사에 비해 더 넓은 인덱스를 탐사하기 때문에 선형 탐사에 비해 연속된 주소들이 채워지는 현상이 덜 발생하게 됩니다.
다만, 제곱 탐사는 동일한 해시 값을 가진 다른 키들이 동일한 탐색 경로를 가지게 되어, 2차 클러스터링(Secondary Clustering) 문제를 여전히 가지고 있습니다.
1차 클러스팅, 2차 클러스팅
1차 클러스터링 (Primary Clustering)
1차 클러스터링은 연속된 주소들이 채워지면서 큰 연속 블록(클러스터)을 형성하는 현상을 말합니다.
이러한 클러스터는 새로운 키가 삽입될 때 더 많은 충돌을 유발하며, 이는 해시 테이블의 성능을 저하시킵니다.
2차 클러스터링 (Secondary Clustering)
2차 클러스터링은 동일한 해시 값에서 시작한 키들이 동일한 탐색 경로를 따르게 되어, 특정 해시 값에 대해 유사한 패턴의 충돌이 반복되는 현상을 말합니다.
3. 이중 해싱(Double Hashing)
이중 해싱(Double Hashing)은 두 개의 서로 다른 해시 함수를 사용하여 충돌이 발생할 경우 데이터를 저장할 새로운 위치를 결정합니다.
즉, 1차 해시 함수는 처음 해시 값을 찾아 저장하기 위해 사용되고, 2차 해시 함수는 해시 값이 충돌되었을 때, 새로운 위치를 찾기 위해 사용됩니다.
이를 통해 1차 클러스터링과 2차 클러스터링 문제를 효과적으로 줄일 수 있습니다.
체이닝(Chaining)
체이닝(Chaining)은 각 슬롯(버킷)에 연결 리스트를 사용하여 동일한 해시 값을 가진 여러 요소들을 저장하는 방식입니다.
이로 인해 충돌이 발생하더라도 추가적인 메모리 공간을 사용하여 데이터를 저장할 수 있습니다.
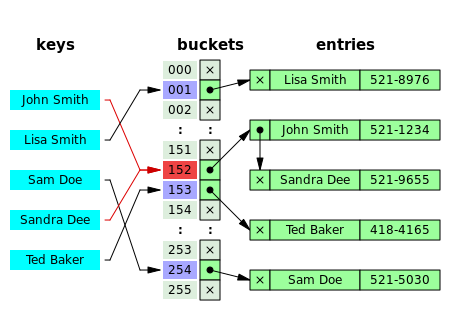
예를 들어, 위에서 152번 인덱스에 충돌이 발생하면, 기존 ‘John Smith’의 데이터 다음에 연결 리스트를 통해 ‘Sandra Dee’가 저장되는 방식입니다.
체이닝의 장점
- 동적 크기 조정: 체이닝은 연결 리스트를 사용하므로 버킷 내에 요소가 추가될 때마다 동적으로 크기를 조정할 수 있습니다.
- 충돌 관리: 충돌이 발생해도 동일한 해시 값을 가진 모든 요소를 버킷의 연결 리스트에 저장할 수 있으므로 충돌 문제를 효과적으로 관리할 수 있습니다.
체이닝의 단점
- 추가 메모리 사용: 연결 리스트를 사용하기 때문에 추가적인 메모리 공간이 필요합니다.
- 탐색 시간 증가: 최악의 경우, 모든 요소가 동일한 버킷에 저장되면 연결 리스트의 길이가 길어져 탐색 시간이 $O(N)$이 될 수 있습니다.
- 캐시 성능 저하: 연결 리스트의 노드들이 메모리의 다른 위치에 저장되므로 캐시 성능이 저하될 수 있습니다.
체이닝의 성능
체이닝 방식의 성능은 해시 테이블의 적재율(Load Factor) 에 크게 영향을 받습니다.
적재율은 다음과 같이 정의됩니다.
\[\frac{n}{m}\]여기서 $n$은 저장된 키-값 쌍의 수, $m$은 해시 테이블의 버킷 수입니다.
즉, 모든 해시 테이블이 가득 적재 되었을 경우 1, 빈 공간이 남을수록 0에 가깝고, 충돌로 인해 과적될 경우 1을 넘어가게 됩니다.
이때, 연결 리스트의 평균 길이를 $\alpha$라고 하면 $\alpha$는 다음과 같이 정의될 수 있습니다.
\[\alpha=\frac{n}{m}\]즉, 충돌이 발생해서 연결리스트가 길어지면 길어질수록 $\alpha$값은 증가하게 되고, 탐색, 삽입, 삭제의 평균 시간 복잡도는 $O(1 + \alpha)$가 됩니다.
이때, 모든 키가 동일한 해시 값을 가지게 되면 연결 리스트의 길이는 $n$이 되고, 이 경우 탐색, 삽입, 삭제의 시간 복잡도는 $O(N)$이 됩니다.